Introduction to the LAST programming language

Darius J Chuck

2022-09-01

2023-11-28 update: added Advanced playground.

2024-02-29 update: added Addendum

Inspired by John Tromp’s remarkable 206-bit self-interpreter for Binary Lambda Calculus (BLC), which I found via Justine Tunney’s amazing SectorLambda, I got an idea for a minimal programming language.

The language is called LAST and this is an introduction to it.

What is it?

LAST is an elegant encoding for lambda calculus which uses no explicit variables or indices and only 4 symbols: L, A, S, and T.

LAST maps trivially to binary and has a BLC-style self-interpreter which is only 194 bits long.

LAST features S-optimization which is a novel form of expression reduction and equivalence, not possible in other variants of lambda calculus.

How does it look like?

To get a visual sense of the language, below are a few classic lambda calculus functions written in LAST.

name	lambda calculus	LAST
identity	λx.x	LT
Y combinator	λf.(λx.f (x x)) (λx.f (x x))	LALASTATTLASTATT
Church encoding
true	λx.λy.x	LLST
false	λx.λy.y	LLT
successor	λn.λf.λx.f (n f x)	LLLASTAASSTSTT
plus	λm.λn.λf.λx.m f (n f x)	LLLLAASSSTSTAASSTSTT
pair	λx.λy.λz.z x y	LLLAATSSTST

For a more complicated function, see the LAST self-interpreter.

Design

Syntax

The formal grammar of the language is as follows (in ABNF):

Term = "L" Term / "A" Term Term / "S" Term / "T"

So a Term (an expression) in LAST is either:

Lambda followed by another Term (the body of the lambda)
Application followed by two consecutive Terms. The first represents the function to apply, the second represents the argument to pass to the function.
Skip followed by another Term (the body of the skip).
Top

Semantics

The semantics are defined by the LAST machine, which is a slightly simplified Krivine machine. The difference is that instead of using de Bruijn indices, the machine uses two simple (albeit more powerful) primitives: S and T (explained below).

The operation of the machine is described in detail in the following section. It is mostly the same as the Krivine machine, so you may skip to the next section if you are already familiar with it. Conversely, you can use descriptions of the Krivine machine to understand the LAST machine.

The LAST machine

The machine state is initialized with the expression to be evaluated and two stacks: one for arguments, one for current environment (typically both empty). Pseudocode type of the machine state is thus:

state = expression * arguments * environment

Both stacks will contain pairs, each made of an expression together with an environment. Such a pair is called a closure.

arguments = stack of closure
environment = stack of closure
closure = expression * environment

The machine loops until the current expression is a Lambda and the argument stack is empty (that’s the stop condition). The result of the evaluation is the expression together with the environment stack.

Every iteration of the loop changes the machine state according to the current expression, as follows:

Lambda causes the machine to stop if the stop condition is met. Otherwise a closure is moved from the top of the argument stack to the top of the environment stack. The current expression becomes the body of the lambda.
Application causes the machine to push a new closure onto the argument stack. The closure is made of the argument expression together with the current environment. The current expression becomes the function expression.
Skip causes the machine to pop a closure off the environment stack. The current expression becomes the body of the skip.
Top causes the machine to pop a closure off the environment stack. The current environment becomes the closure’s environment. The current expression becomes the closure’s expression.

Before interpreting S or T the environment stack must be nonempty – otherwise the machine stops with an error.

Correspondence between LAST and lambda calculus with de Bruijn indices

The Krivine machine interprets lambda calculus with de Bruijn indices. These indices are natural numbers which identify variables in the environment stack.

Instead of numerical indices LAST uses two primitives (S and T) which can emulate them: T is equivalent to 0 and S is equivalent to the successor function.

In other words, indices can be translated into LAST as follows:

The index 0 is translated into T
An index n + 1 is translated to S followed by a translation of index n

Meaning an index n is n repetitions of S followed by a T. For example:

index	in BLC	in LAST
0	10	T
1	110	ST
2	1110	SST
3	11110	SSST
4	111110	SSSST
5	1111110	SSSSST

This shows that the LAST machine can fully emulate the Krivine machine.

However the Krivine machine cannot fully emulate the LAST machine, as S can also precede L and A (semantics explained in S-optimization).

In effect, all programs in BLC can be translated to LAST, but not vice versa.

Therefore LAST can be seen as a superset of lambda calculus with de Bruijn indices.

S-optimization

LAST introduces the notion of S-optimization which is a kind of optimization that can turn some programs into shorter and more efficient equivalents.

The ability to encode these more efficient equivalents is unique to LAST.

S-optimization can be automated, so a compiler from BLC (or a higer-level language) to LAST is viable.

S-deoptimization, an inverse of S-optimization, can also be automated, so a compiler from LAST to BLC or lambda calculus with de Bruijn indices is also viable.

To explain S-optimization, let’s take the following lambda expression:

λx.λy.x x

which can be encoded for the Krivine machine as:

λλ 1 1

This in turn can be translated to LAST as:

LLASTST

However, there is also an equivalent, yet shorter and more efficient equivalent program which can be written in LAST, but not lambda calculus with de Bruijn indices:

LLSATT

The difference is that the S has been “factored out” of the A: an unused variable on top of the stack has been discarded before applying the variable below to itself. This has been done only once as opposed to two times in the previous program.

This may be easier to explain with a visualization:

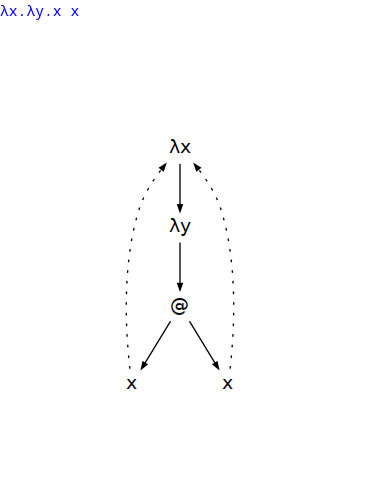
Screenshot from the Lambda Viewer by Hai (Paul) Liu

Screenshot from Hai (Paul) Liu’s Lambda Viewer tool

As we can see x is referred to twice in the application while y is not referred to at all, but “stands in the way”. With de Bruijn indices and Krivine machine we have no choice but to implicitly skip over it twice while in LAST we can skip over only once.

The ability to do this in LAST enables more efficient and shorter programs. The more variables stand in the way and the more references to variables that precede them, the more the length of the program is reduced and the efficiency improved. For a slightly more complex example:

λx.λy.λz.x x x x
; before optimization:
LLLAAASSTSSTSSTSST
; after optimization:
LLLSSAAATTTT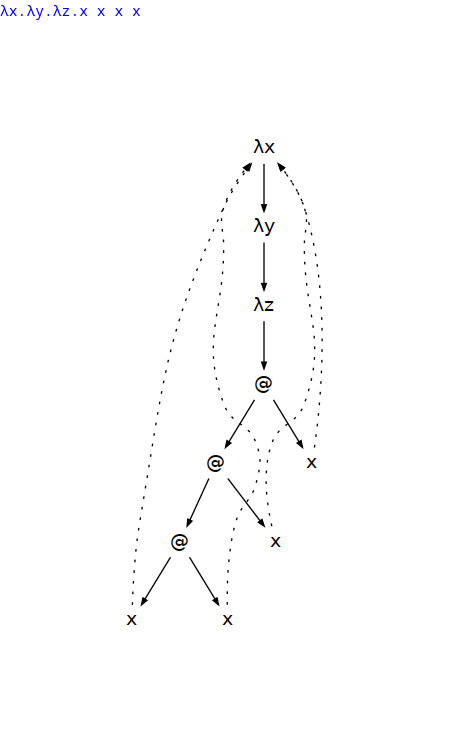

Screenshot from Hai (Paul) Liu’s Lambda Viewer tool

As we can see we have 4 references to x and 2 variables (y and z) to skip over.

A nontrivial example of an S-optimized program is presented in the section BLC-style LAST self-interpreter.

LAST programs are quaternary numbers

If we consider the symbols L, A, S, T to be digits, a LAST program is a number in quaternary.

For example:

LALASTATTLASTATT

is equivalent to the bijective quaternary number:

1212342441234244

where we map:

L <-> 1
A <-> 2
S <-> 3
T <-> 4

BLC-style I/O

We shall now define an I/O protocol for LAST similar to that of BLC, except input and output in it will be a string of quaternary digits rather than bits.

For example the following LAST program:

LTLALALA

will output LALALA.

The program has 2 parts (separated by space for clarity):

LT LALALA

The first part, LT, is the main function (which is the identity function).

The second part, LALALA, is the input string.

Upon execution, the input is converted to a list of digits as follows.

Each digit is converted to a function which represents it:

L = LLLLSSST
A = LLLLSST
S = LLLLST
T = LLLLT

These functions are then paired together into a list (in pseudocode):

pair(L,
  pair(A,
    pair(L,
      pair(A,
        pair(L,
          pair(A,
            NIL
          )
        )
      )
    )
  )
)

where pair is the standard pairing function, which is represented in LAST as:

pair = LLLAATSSTST

and NIL is identical to the standard false function:

NIL = LLT

The result of this conversion for our LALALA example can be represented in LAST as (whitespace for clarity):

LAAT LLLLSSST
LAAT LLLLSST
LAAT LLLLSSST
LAAT LLLLSST
LAAT LLLLSSST
LAAT LLLLSST
LLT

This list is then fed to the main function.

The main function should operate on that input and then output a result as a similar list of digits. Here the operation is identity, so the input is turned directly into output without change. So the output of our main function will be exactly the same list:

LAAT LLLLSSST
LAAT LLLLSST
LAAT LLLLSSST
LAAT LLLLSST
LAAT LLLLSSST
LAAT LLLLSST
LLT

That list is then converted back to digits and displayed:

LALALA

BLC-style LAST self-interpreter

The operation of the BLC self-interpreter is explained in detail in this paper.

A similar albeit more efficient self-interpreter for LAST is 97 characters:

ALATTLALLLATSLAAAATSASTLASTLLASSTLAATSTSSTSASTLASS
TLASSTLAASSTTASTTSASTLASTLASTATLLTSATLATLLSTATT

The general interface of the interpreter is the same, except that thanks to the quaternary I/O (which fits neatly with the LAST syntax) as well as S-optimization it is more streamlined and efficient than the original.

Moreover, as we shall see, it can be trivially compressed into 194 bits, surpassing the original by 12 bits.

Trivial binary encoding

Since LAST programs are quaternary numbers, there is a trivial mapping between LAST and binary:

L <-> 00
A <-> 01
S <-> 10
T <-> 11

LAST-B: binary LAST

With the above mapping to binary, we can define LAST-B – a binary version of LAST which works exactly the same, except it uses binary rather than quaternary.

Since each quaternary digit turns into two binary digits, every LAST-B program fits into an even number of bits and the length of a LAST-B program in bits is twice the length of the equivalent LAST program.

This is unlike BLC, where odd de Bruijn indices take odd number of bits, so programs can have an odd length. The advantage of BLC indices is that they are shorter than LAST-B “indices” (index n is shorter by n bits).

The 194-bit LAST-B self-interpreter

Having defined LAST-B, we can now translate the 97-character BLC-style LAST self-interpreter:

ALATTLALLLATSLAAAATSASTLASTLLASSTLAATSTSSTSASTLASS
TLASSTLAASSTTASTTSASTLASTLASTATLLTSATLATLLSTATT

into 194 bits:

01000111110001000000011110000101010111100110110001
10110000011010110001011110111010111001101100011010
11000110101100010110101111011011111001101100011011
00011011011100001110011100011100001011011111

Simple playground

Enter LAST code or select an example and click one of the buttons below*.

Example:

All characters except L, A, S, and T will be ignored.

run

run and render as LAST-B (binary)

S-optimize

S-deoptimize

Output will appear here.

* Note: input goes immediately after the program and is not interactive. For a more advanced playground with interactive input, see nuklĕus below.

Advanced playground

nuklĕus is a minimal web-based IDE for LAST with a debugger, where you can compile LAST programs to a very closely-related virtual machine bytecode which can then be executed step-by-step. The debugger visualizes the state of memory at each step and supports interactive I/O.

To open nuklĕus, click on the screenshot below.

Addendum 2024-02-29

Since publishing this article, I have exchanged some correspondence with John Tromp, mentioned at the beginning, who expressed an interest LAST. He was particularly interested in the idea of splitting de Bruijn indices into independent 0 and successor operations.

Digging in the literature, John discovered that the same idea was described by Ross Paterson and Richard Bird in 2000 in the article “De Bruijn notation as a nested datatype” (section 5).

This article, in turn, referred to another one, from a 1991 conference, by the same Paterson: “A Tiny Functional Language with Logical Features”. I looked up this article in the conference proceedings and found on page 76 a syntax definition similar to this:

e ::= "0" | "S" e | e_1 e_2 | "λ" e

Indeed, it’s basically the same idea! Officially scientifically validated. ;)

Interestingly, one day after receiving this information, quite accidentally (!), while browsing the Wikipedia article on interaction nets, I came across the work “Lambdascope: Another optimal implementation of the lambda-calculus” (van Oostrom, Vincent; van de Looij, Kees-Jan; Zwitserlood, Marijn (2010)), where on page 2 I found the following definition:

Here a generalised λ-term, as introduced in [4], is a λ-term where successors are generalised to be applicable to any (generalised) term instead of just to De Bruijn indices […]

Formally, the grammar for the set GΛ of generalised λ-terms is
t ∈ GΛ ::= 0 | St | λt | tt

Same idea again! The reference under [4] here sends to “R. Bird and R. Paterson. De Bruijn notation as a nested datatype. Journal of Functional Programming, 9(1):77–91, 1999”, an earlier version of the article found by John!